
ยินดีต้อนรับทุกท่าน เข้าสู่ เว็บแทงหวยออนไลน์ 999LUCKY164 เล่นง่าย มีอัตราจ่ายสูงมิติใหม่ของ วง การหวยออนไลน์
เว็บหวยออนไลน์ชั้นนำอันดับหนึ่ง บริการรับแทงหวยทุกชนิด ! หวยรัฐบาล หวยลาว หวยใต้ดิน หวยฮานอยออนไลน์ หวยจับยี่กี หวยหุ้นไทย เเละยังมีหวยน้องใหม่อย่าง หวยลัคกี้เฮง เเทงหวยกับเรา 999LUCKY สมัครฟรี ไม่มีค่าใช่จ่ายไดๆ ทั้งสิ้น !!
ขอต้อนรับสมาชิกใหม่ทุกท่าน เข้าสู่ระบบ เว็บแทงหวยออนไลน์ ครบวงจรที่ดีที่สุด อันดับ 1 ที่มาแรงที่สุด ในประเทศไทย ขณะนี้ สมัครเล่นหวยออนไลน์ ซื้อหวยออนไลน์ ราคาดี อัตราจ่ายสูงที่สุด และมีระบบแทงหวย ที่ทันสมัยและยิ่งใหญ่ที่สุด ถือว่าเป็นเจ้าแรกๆที่เข้ามาเปิดให้บริการ คนไทยเลยก็ว่าได้ แทงหวยได้โดยไม่มีขั่นต่ำ1บาท ก็สามารถ แทงหวยได้ 999LUCKY เล่นง่าย จ่ายจริง ราคาดี จ่ายสูง ไม่โกง !!
ซื้อหวยกับ 999LUCKY ซื้อหวยออนไลน์ อัตราการจ่ายสูง จ่ายสูงถึงบาทละ 800 บริการหวยออนไลน์ครบวงจร มีหวยออนไลน์ทุกชนิด รวมอยู่ใน 999LUCKY มีที่นี้ที่เดียว มีหวยออนไลน์ ให้ท่านเลือกเล่นมากมาย ไม่ว่าจะเป็น หวยรัฐบาล หวยฮานอย หวยลาว Huay หวยมาเลย์ หวยสิงคโปร์ หวยปิงปอง หวยจับยี่กี หวยหุ้นไทย หวยหุ้นประเทศ ต่างๆ หวยลัคกี้เฮง และยังมีหวยอื่นๆ อีกมากมายให้ท่านได้เล่นเล่นกัน สมัครแทงหวยออนไลน์ กับ 999LUCKY ท่านจะได้รับ โปรโมชั่น และสิทธิพิเศษอีกมากมาย !
เว็บแทงหวยออนไลน์ 999LUCKY การเงิน มั่นคง มี ระบบ ฝาก-ถอน ที่ทันสมัย รวดเร็ว ทันใจ ปลอดภัยชัวร์ 100 %
สำหรับ 999LUCKY ยังมาพร้อม ระบบ ฝาก-ถอน อัตโนมัติ ฝากถอน ได้ โดยไม่มีขั่นต่ำ รวดเร็ว ทันใจ ฝากเงิน ไปปรับยอดเครดิตได้เร็วมาก ถอนเงิน ก็ถอนออกง่ายทัน ใจสามารถทำการกับเว็บไซต์เราได้ ตลอด 24 ชั่วโมง ครับ !!
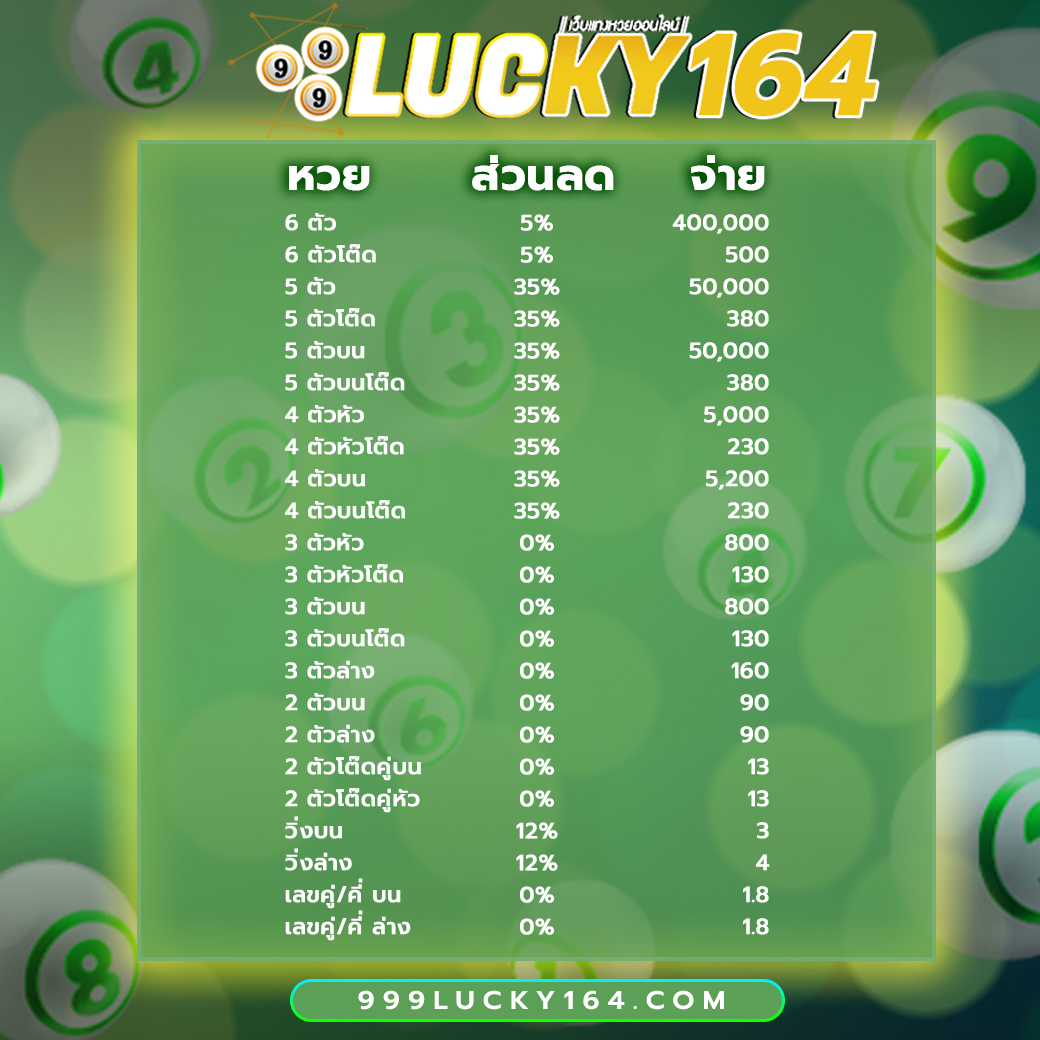
โปรโมชั่นหวยลดสูงสุด 33% จ่ายมากที่สุด 550 แทงหวยปลอดภัยมั่นใจเรื่อง การเงินการันตีจากเซียนหวย ทั่วประเทศ
3 ตัว ลดสูงสุด 33% จ่าย 550 บาท
2 ตัวบนและล่าง ลดสูงสุด 28% จ่าย 70 บาท
3 ตัวล่าง จ่าย 125 บาท
วิ่งอัตราลด 12%
3 ตัวโต๊ด จ่าย 105 บาท
2 ตัวโต๊ด จ่าย 12 บาท
แทงขั้นต่ำเพียง 10 บาทเท่านั้น
สมัครแทงหวยออนไลน์ กับ 999lucky วันนี้ท่านจะได้ สิทธิพิเศษเเละ โปรโมชั่น อีกมากมายจากทางเว็บ เพียบ จ้า !
จุดเด่นของเว็บหวยออนไลน์ 999LUCKY คือเปิดบริการรับแทงหวยซื้อหวยออนไลน์ชั้นนำ กับเราเพราะมีความมั่นคง ด้านการเงินปลอดภัย 100% แถมยังมี อัตราการจ่ายสูง จ่ายสูงถึงบาทละ 800 ส่วนลดเยอะ จ่ายเงินแล้วเล่นได้เงินจริง จ่ายเต็ม ไม่มีโกง แน่นอนครับ !!
ทางเข้าแทงหวย999LUCKY
วิธีสมัครสมาชิก
วิธีฝากเงิน
วิธีถอนเงิน
ติดต่อเรา999LUCKY
สำหรับท่านลูกค้าท่านใดที่กำลังมองหา เว็บแทงหวยที่ดีที่สุด ในตอนนี้ผมจึงขอนำเสนอ เว็บแทงหวย999Lucky การันตรีความปลอดภัย มั่นคง100% คับท่าน !
999luckyเว็บแทงหวยชั้นนำอันดับ 1 ในประเทศไทย 2022
แถมยังมีระบบ ฝาก-ถอน อัตโนมัต มั่นคง ปลอดภัย เเละ จ่ายจริง ไม่โกง 100 %
หวยยี่กี| หวยออนไลน์| หวยรัฐบาล| หวยฮานอย| หวยมาเลย์

